Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- java
- 안드로이드스튜디오
- 혼공단
- 코틀린
- Android
- CS
- 프로그래머스
- groupby
- 안드로이드
- 알고리즘
- join
- 혼공파
- 정보처리기사
- 카카오코테
- Til
- 혼공챌린지
- 자료구조
- 자바
- 오블완
- 기술면접
- 스터디
- 인프런
- 티스토리챌린지
- select
- 코테
- SQL
- Kotlin
- MySQL
- doitandroid
- 정처기
Archives
- Today
- Total
Welcome! Everything is fine.
[Algorithm/Study] 4주차 - 트리 본문
728x90
해당 스터디는 <코딩 테스트 합격자 되기 C++> 저자님과 함께하는 스터디입니다.
인프런 강의 < 코딩 테스트 합격자 되기 C++ > 을 보고 정리한 내용입니다.
트리의 개념
강의를 보며 직접 트리를 그려 간단한 개념을 정리해보았다.

- 트리 : 노드(Node)와 간선(Edge)으로 이루어진 계층적 자료구조, 그래프의 한 종류이며 순환을 허용하지 않는다.
- 노드 : 트리의 각 구성 요소
- 간선 : 노드와 노드를 연결하는 선
- 루트 노드 : 트리에서 유일한 노드, 최상위 노드
- 부모 노드 : 자식 노드를 직접 연결하고 있는 상위 노드
- 자식 노드 : 특정 노드로부터 직접 연결된 하위 노드
- 형제 노드 : 같은 부모 노드를 가진 노드
- 리프 노드 : 자식 노드가 없는 노드, 트리의 끝
- 차수 : 특정 노드가 가진 자식 노드의 개수(위 그림에서 루트 노드의 차수는 3)
- 이진 트리 : 자식 노드가 최대 2개인 트리
트리 표현 - 배열
- 루트 노드 인덱스는 1
- 배열 인덱스 0부터 사용할 수도 있지만 딱히 효율은 없음
- 왼쪽 자식 노드는 부모 노드 인덱스 * 2
- 오른쪽 자식 노드는 부모 노드 인덱스 * 2 + 1
장점
- 인덱스 공식만 활용하므로 구현 난이도가 낮다.
단점
- 빈 공간이 많아서 메모리 공간을 낭비할 수 있다.(구현은 쉽지만..)
트리 표현 - 인접 리스트
- 각 리스트의 인덱스는 부모 노드
- 자식 노드는 부모 노드에 해당되는 인덱스에 추가
장점
- 배열보다 공간 효율이 좋다.
단점
- 자식 노드를 찾는데 오래 걸릴 수 있다.
- 순차 탐색 필요, N번째 노드까지 탐색하는 데 오래 걸린다.
이진 트리의 순회
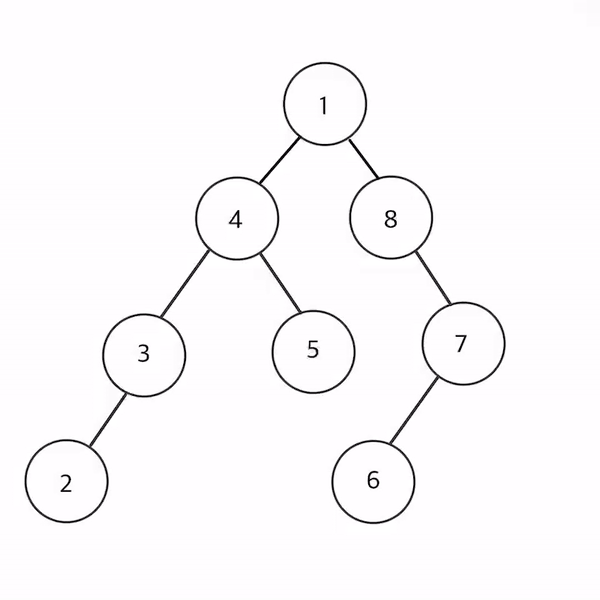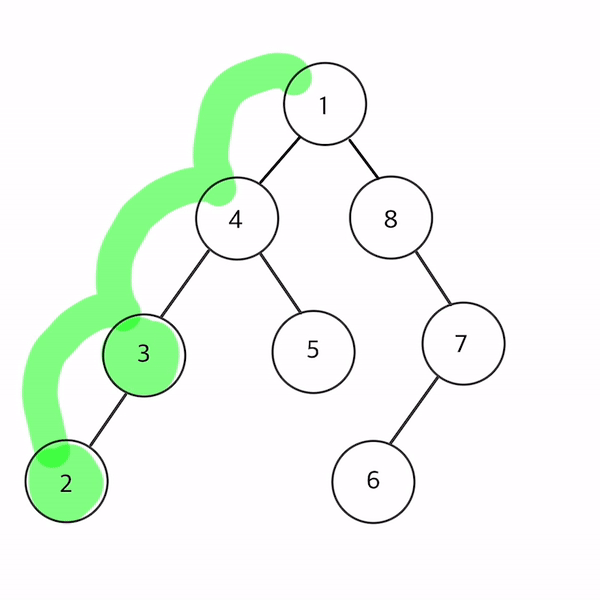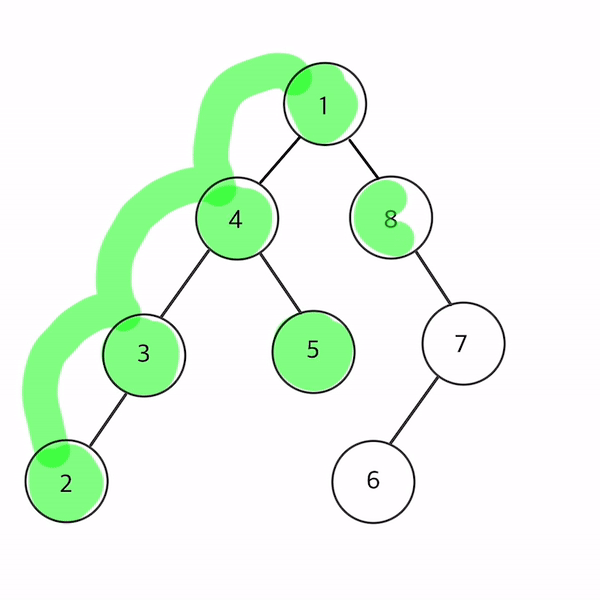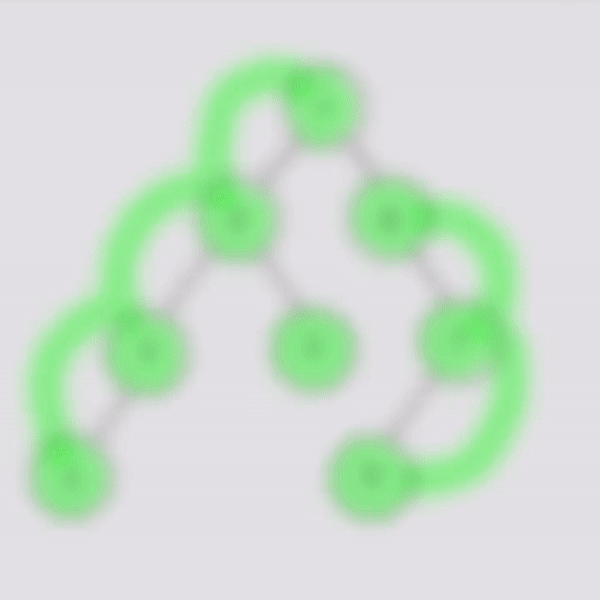
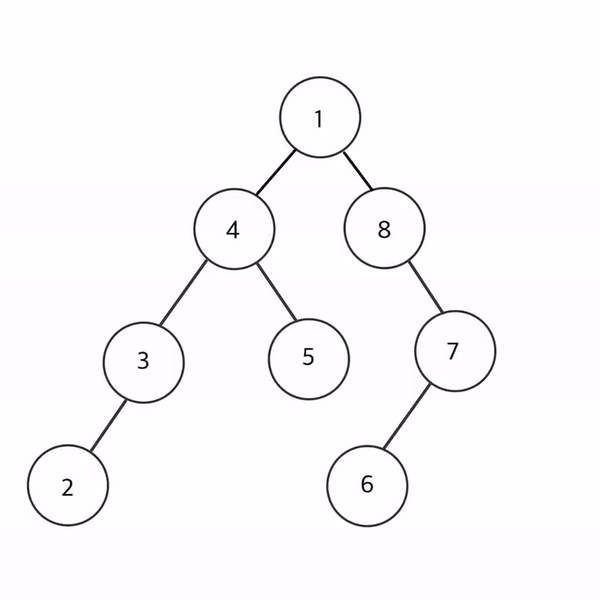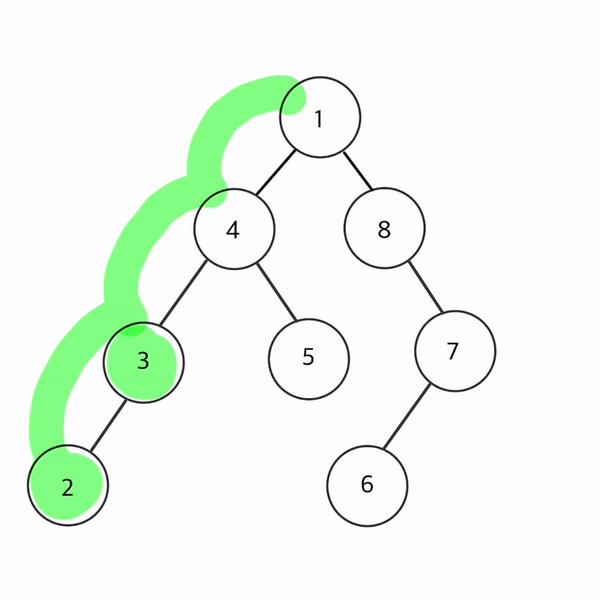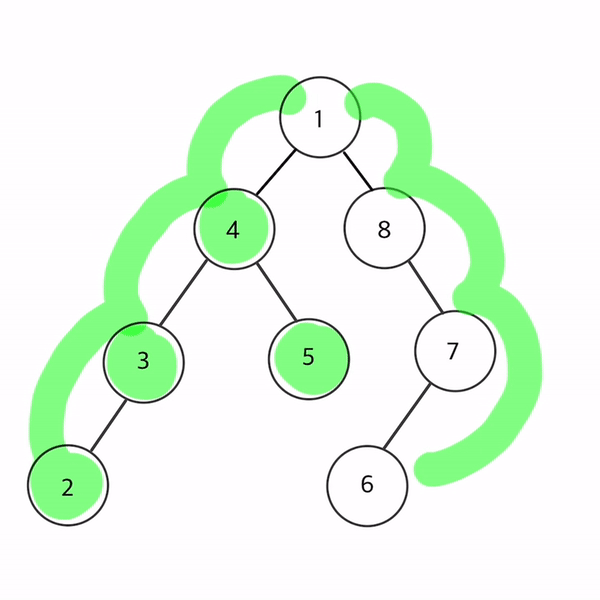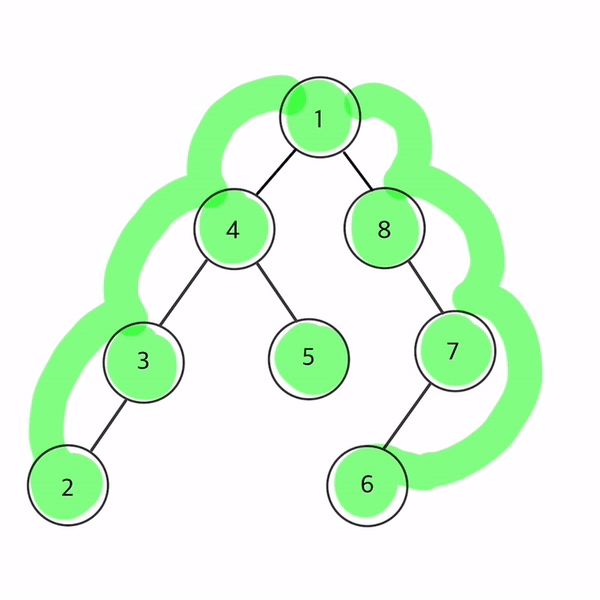
현재 노드를 언제 방문하는지에 따라 전위 순회, 중위 순회, 후위 순회로 분류된다. 다음 트리를 가지고 전위 순회, 중위 순회, 후위 순회를 해보자!
1
/ \
4 8
/ \ \
3 5 7
/ /
2 6
예시 트리를 배열로 표현하면 다음과 같이 된다.

전위 순회
- 부모 노드 → 왼쪽 자식 노드 → 오른쪽 자식 노드 순으로 진행된다.
- 순차적으로 노드를 순회하므로 트리를 복사할 때 사용된다.
- 1 → 4 → 3 → 2 → 5 → 8 → 7 → 6 순으로 순회
트리를 직접 그려 전위순회를 따라 노드를 칠해보았다!
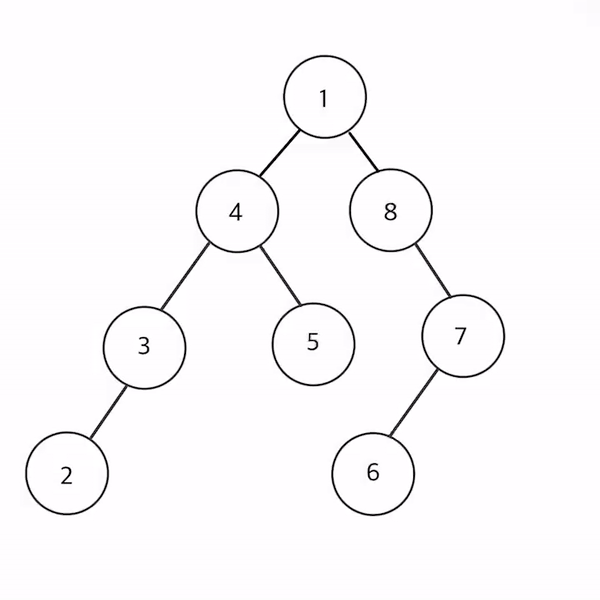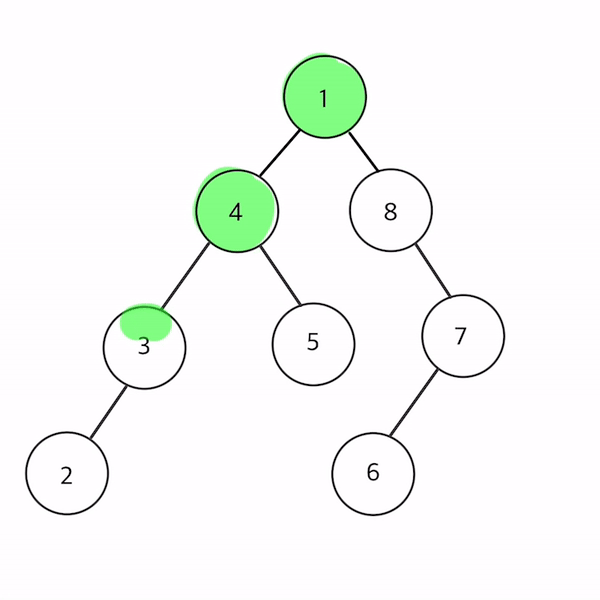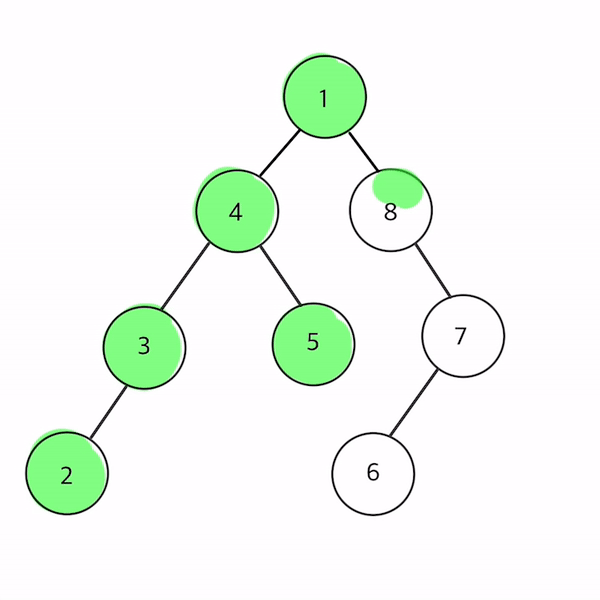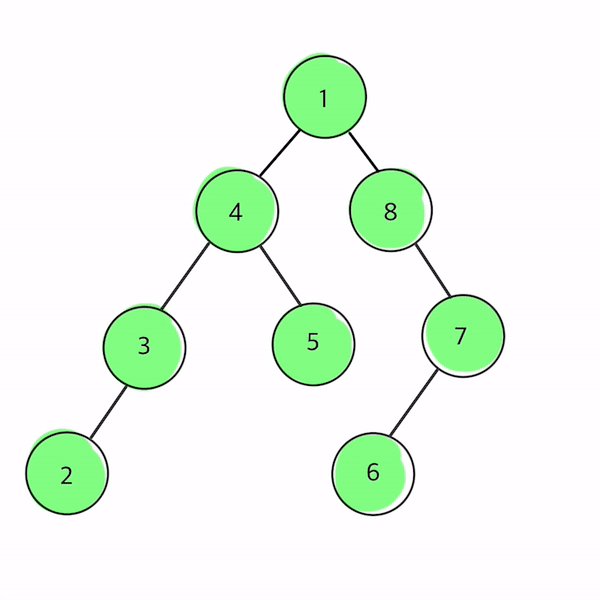
자바로 구현한 전위 순회이다.
public class BinaryTreeArray {
int[] tree;
int size;
public BinaryTreeArray(int size) {
this.size = size;
tree = new int[size + 1]; // 인덱스 1부터 시작하므로 크기 1 더 추가
}
// 배열에 값을 삽입하는 메서드
public void insert(int index, int value) {
if (index < size + 1) {
tree[index] = value;
} else {
System.out.println("인덱스가 트리의 크기를 초과합니다.");
}
}
// 전위 순회 메서드
public void preorder(int index) {
if (index >= size + 1 || tree[index] == 0) {
return;
}
// 현재 노드 방문
System.out.print(tree[index] + " ");
// 왼쪽 자식 방문
preorder(2 * index);
// 오른쪽 자식 방문
preorder(2 * index + 1);
}
public static void main(String[] args) {
BinaryTreeArray tree = new BinaryTreeArray(10);
// 트리 구성 (인덱스 1부터 시작)
tree.insert(1, 1); // 루트 노드
tree.insert(2, 4); // 루트의 왼쪽 자식
tree.insert(3, 8); // 루트의 오른쪽 자식
tree.insert(4, 3); // 노드 4의 왼쪽 자식
tree.insert(5, 5); // 노드 4의 오른쪽 자식
tree.insert(7, 7); // 노드 8의 오른쪽 자식
tree.insert(8, 2); // 노드 3의 왼쪽 자식
tree.insert(10, 6); // 노드 7의 왼쪽 자식
// 전위 순회 출력
System.out.println("전위 순회 결과:");
tree.preorder(1); // 인덱스 1부터 시작
}
}중위 순회
- 왼쪽 자식 노드 → 부모 노드 → 오른쪽 자식 노드 순으로 진행된다.
- 이진탐색트리 원소를 정렬된 상태로 순회할 때 사용된다. 왼쪽은 부모보다 작고, 오른쪽은 크기 때문에 왼쪽 자식 노드 → 부모 노드 → 오른쪽 자식 노드 순으로 방문하는 것을 재귀적으로 하면 정렬된 상태로 순회할 수 있다.
- 2 → 3 → 4 → 5 →1 → 8 → 6 → 7 순으로 순회
자바로 구현한 중위 순회이다.
public class BinaryTreeArrayInorder {
int[] tree;
int size;
public BinaryTreeArrayInorder(int size) {
this.size = size;
tree = new int[size + 1]; // 인덱스 1부터 시작하므로 크기 1 더 추가
}
// 배열에 값을 삽입하는 메서드
public void insert(int index, int value) {
if (index < size + 1) {
tree[index] = value;
} else {
System.out.println("인덱스가 트리의 크기를 초과합니다.");
}
}
// 중위 순회 메서드 (Inorder)
public void inorder(int index) {
if (index >= size + 1 || tree[index] == 0) {
return;
}
// 왼쪽 자식 방문
inorder(2 * index);
// 현재 노드 방문
System.out.print(tree[index] + " ");
// 오른쪽 자식 방문
inorder(2 * index + 1);
}
public static void main(String[] args) {
BinaryTreeArrayInorder tree = new BinaryTreeArrayInorder(10);
// 트리 구성 (인덱스 1부터 시작)
tree.insert(1, 1); // 루트 노드
tree.insert(2, 4); // 루트의 왼쪽 자식
tree.insert(3, 8); // 루트의 오른쪽 자식
tree.insert(4, 3); // 노드 4의 왼쪽 자식
tree.insert(5, 5); // 노드 4의 오른쪽 자식
tree.insert(7, 7); // 노드 8의 오른쪽 자식
tree.insert(8, 2); // 노드 3의 왼쪽 자식
tree.insert(10, 6); // 노드 7의 왼쪽 자식
// 중위 순회 출력
System.out.println("중위 순회 결과:");
tree.inorder(1); // 인덱스 1부터 시작
}
}후위 순회
- 왼쪽 자식 노드 → 오른쪽 자식 노드 → 부모 노드 순으로 진행된다.
- 제일 깊숙히 들어있는 폴더부터 삭제하는 경우 등에 사용된다.
- 2 → 3 → 5 → 4 → 6 → 7 → 8 → 1 순으로 순회
자바로 구현한 후위 순회이다.
public class BinaryTreeArrayPostorder {
int[] tree;
int size;
public BinaryTreeArrayPostorder(int size) {
this.size = size;
tree = new int[size + 1]; // 인덱스 1부터 시작하므로 크기 1 더 추가
}
// 배열에 값을 삽입하는 메서드
public void insert(int index, int value) {
if (index < size + 1) {
tree[index] = value;
} else {
System.out.println("인덱스가 트리의 크기를 초과합니다.");
}
}
// 후위 순회 메서드 (Postorder)
public void postorder(int index) {
if (index >= size + 1 || tree[index] == 0) {
return;
}
// 왼쪽 자식 방문
postorder(2 * index);
// 오른쪽 자식 방문
postorder(2 * index + 1);
// 현재 노드 방문
System.out.print(tree[index] + " ");
}
public static void main(String[] args) {
BinaryTreeArrayPostorder tree = new BinaryTreeArrayPostorder(10);
// 트리 구성 (인덱스 1부터 시작)
tree.insert(1, 1); // 루트 노드
tree.insert(2, 4); // 루트의 왼쪽 자식
tree.insert(3, 8); // 루트의 오른쪽 자식
tree.insert(4, 3); // 노드 4의 왼쪽 자식
tree.insert(5, 5); // 노드 4의 오른쪽 자식
tree.insert(7, 7); // 노드 8의 오른쪽 자식
tree.insert(8, 2); // 노드 3의 왼쪽 자식
tree.insert(10, 6); // 노드 7의 왼쪽 자식
// 후위 순회 출력
System.out.println("후위 순회 결과:");
tree.postorder(1); // 인덱스 1부터 시작
}
}이진 탐색 트리(Binary Search Tree, BST)
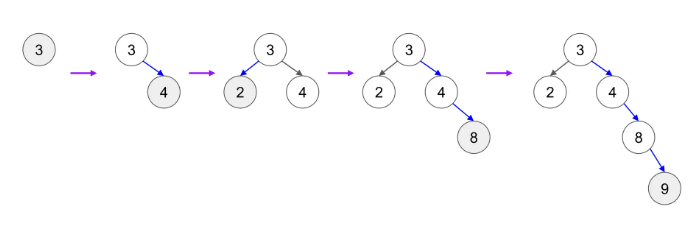
- 이진 탐색 트리 : 탐색을 효율적으로 하기 위해 만든 이진 트리
- 왼쪽 트리 - 부모 노드보타 작은 값, 오른쪽 트리 - 부모 노드보다 큰 값
- 평균적으로 O(logN), 최악의 경우 O(N)의 시간 복잡도를 가진다. (최악의 경우에는 트리 높이만큼 탐색하기 때문)
- 삽입과 동시에 정렬을 한다.
- 자바에서 TreeMap, TreeSet의 경우 내부적으로 균형 이진 트리(레드-블랙 트리)를 사용한다.
'Algorithm' 카테고리의 다른 글
| [Algorithm/Study] 6주차 - 그래프 (10) | 2024.11.10 |
|---|---|
| [Algorithm/Study] 5주차 - 집합 (0) | 2024.11.03 |
| [Algorithm/Study] 3주차 - 해시 (0) | 2024.10.19 |
| [Algorithm/Study] 2주차 - 스택과 큐 (0) | 2024.10.12 |
| [Algorithm/Study] 1주차 - 시간복잡도 (2) | 2024.10.04 |




