| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 혼공파
- 코틀린
- 혼공단
- 정처기
- 프로그래머스
- join
- 안드로이드
- 혼공챌린지
- select
- MySQL
- Android
- 티스토리챌린지
- 자료구조
- 스터디
- 코테
- 자바
- SQL
- 기술면접
- 카카오코테
- CS
- Kotlin
- 오블완
- java
- groupby
- doitandroid
- 인프런
- 안드로이드스튜디오
- 정보처리기사
- 알고리즘
- Til
- Today
- Total
Welcome! Everything is fine.
[Algorithm/Study] 5주차 - 집합 본문
해당 스터디는 <코딩 테스트 합격자 되기 C++> 저자님과 함께하는 스터디입니다.
인프런 강의 < 코딩 테스트 합격자 되기 C++ > 을 보고 정리한 내용입니다.
상호배타적 집합
상호배타적 집합이란 교집합이 없는, 즉 공통원소를 가지지 않는 집합 관계를 의미한다. 예를 들어, 집합 A의 원소가 {1, 2, 3}이고 집합 B의 원소가 {4, 5, 6} 일 때 상호배타적 집합이라고 할 수 있다. 반면, 집합 A의 원소가 {1, 2, 3}이고 집합 B의 원소가 {2, 4, 6}이라면 상호배타적 집합이라고 할 수 없다. 교집합 {2}가 존재하기 때문이다.
상호배타적 집합을 표현할 때 고려해야할 점들은 다음과 같다. 집합 A = {1, 2, 3}, 집합 B = {4, 5, 6}일 때...
- 특정 집합 원소들이 하나의 집합 원소라는 것을 알 수 있어야 한다.
- ex) 각 원소 {1, 2, 3}이 집합 A에 속한다는 것을 알아야 한다.
- 각 집합이 다른 집합이라는 것을 알 수 있어야 한다.
- ex) 집합 A와 B가 다른 집합이라는 것을 알아야 한다.
- 특정 원소가 어느 집합에 속하는지 알 수 있어야 한다.
- ex) 원소 5가 집합 B에 속한다는 것을 확인할 수 있어야 한다.
- 두 개의 집합을 하나로 합칠 수 있어야 한다.
- ex) 두 개의 집합을 합쳐 {1, 2, 3, 4, 5, 6, 7}로 만들 수 있어야 한다.
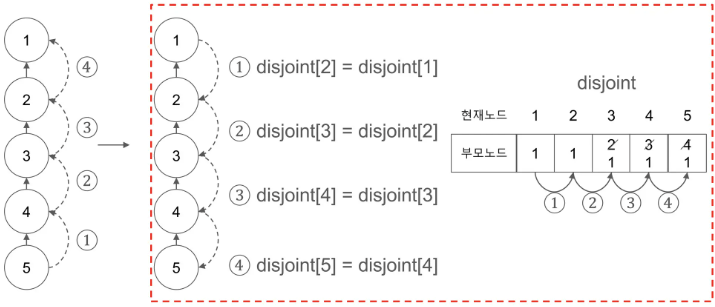
배열을 활용해 집합을 표현할 수 있다. 현재노드는 인덱스, 부모노드는 값으로 표현해 다음과 같이 나타낸다. 각 집합에서 가장 작은 원소를 대표노드(루트노드)로 하고, 대표 원소는 현재노드와 부모노드가 같다. 부모노드가 없다면 -1로 나타낸다.
| 현재노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 부모노드 | 1 | 1 | 1 | 4 | 4 | 4 | -1 | 3 |
집합의 연산
find
find 연산은 특정 노드의 루트노드를 확인하는 연산이다. 특정 노드로부터 루트노드가 나올 때까지 거슬러 올라간다.
예를 들어, 다음과 같은 집합 A가 있을 때 find(7)을 하면 루트노드인 1을 찾을 수 있어야 한다.

- 인덱스와 값을 비교해 같지 않으면 find(부모노드)를 한다.
- 같을 때까지 계속 find를 호출하여 거슬러 올라단다.
- 같으면 인덱스의 값을 부모노드에 넣으면서 다시 올라간다. 그렇게 다시 7까지 오면 7의 부모노드는 1이라는 것을 알 수 있다. 혹은 같으면 바로 해당 값을 리턴시킨다.
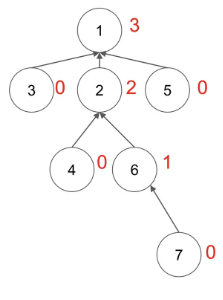
find의 최악의 경우는 다음과 같다. 루트노드를 찾는데 필요한 경로가 깊어질 경우 연산 횟수가 증가하기 때문에 O(N)의 시간복잡도가 걸린다.

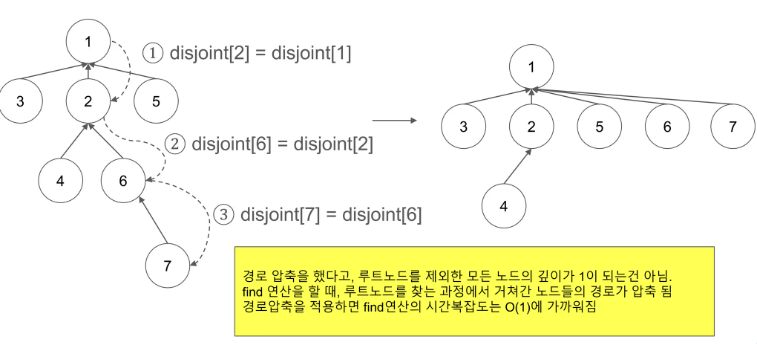
이런 경우에는 경로의 깊이를 줄이기 위해 경로 압축 알고리즘을 활용할 수 있다. 위 집합은 아래처럼 다시 표현할 수 있다. find 연산을 하는 노드가 루트노드일 경우 루트노드를 반환하고, 아닐 경우 자신의 부모노드를 find(해당 노드의 부모노드)로 설정한다.

따라서 경로 압축의 실제 동작은 다음과 같다.
그러나 경로 압축을 했다고 루트노드를 제외한 모든 노드의 깊이가 1이 되는 것은 아니다. find 연산 시 루트노드를 찾는 과정에서 거쳐간 노드들의 경로가 압축된다.find(7)을 한다면, 노드 4는 그대로 있게 된다.
union
union 연산은 두 개의 집합을 하나의 집합으로 합치는 연산이다. find 연산을 통해 각 집합의 대표 원소를 구하고, 루트노드를 하나로 통일한다. 가장 간단한 방법은 다음 그림과 같이 가장 작은 루트노드쪽으로 합치는 방법이 있다.
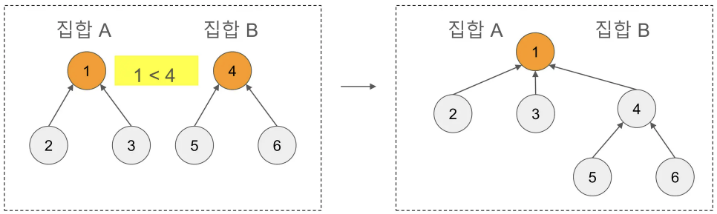
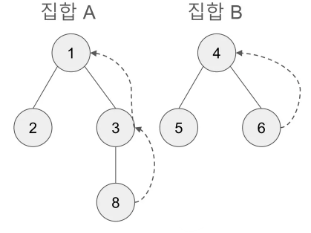
union(6, 8)을 수행하면 find(6), find(8)을 통해 루트노드를 확인한다. find(6)보다 find(8) 작으므로 두 집합의 대표원소를 find(8)로 통일한다.
union 연산을 할 때 집합에 랭크(특정 노드 기준 최대 깊이)를 도입해 깊이를 최소화할 수 있다.랭크가 더 큰 쪽으로 합쳐서 랭크의 증가를 최소화하는 것이 랭크 기반 알고리즘이다.
랭크가 더 높은 쪽으로 합치면 깊이가 더 낮다.
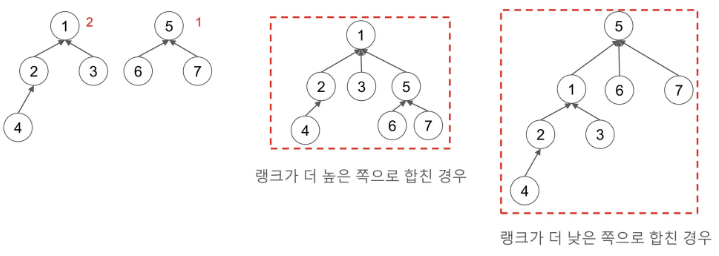
경로압축 / 랭크기반 알고리즘
집합 알고리즘은 언제 쓰일까?
- 이미지 세그먼테이션 - 각 이미지를 의미있는 부분으로 분할
- 네트워크 연결성 확인 - 대규모 네트워크에서 두 컴퓨터가 서로 연결되어 있는지 확인
자바로 구현한 union-find 알고리즘의 예시이다. 그래프에서 연결 요소를 찾거나 사이클을 검출할 때 자주 활용된다.
public class UnionFind {
private int[] parent;
private int[] rank;
// 초기화: 각 노드가 자기 자신을 부모로 가리키며, 랭크는 0으로 초기화
public UnionFind(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i; // 초기에는 각 노드가 자기 자신을 부모로 가짐
rank[i] = 0; // 초기 랭크는 0
}
}
// Find 연산: 경로 압축을 적용하여 루트 찾기
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]); // 경로 압축
}
return parent[x];
}
// Union 연산: 랭크 기반 합치기 적용
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 두 노드의 루트가 같지 않다면 합침
if (rootX != rootY) {
// 랭크 기반 합치기: 랭크가 높은 쪽이 루트가 되도록 함
if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else {
parent[rootY] = rootX;
rank[rootX]++; // 두 랭크가 같다면 하나의 랭크 증가
}
}
}
// 두 원소가 같은 집합에 속하는지 확인
public boolean isConnected(int x, int y) {
return find(x) == find(y);
}
public static void main(String[] args) {
UnionFind uf = new UnionFind(10);
// 유니온 연산
uf.union(1, 2);
uf.union(2, 3);
uf.union(4, 5);
uf.union(6, 7);
uf.union(5, 6);
uf.union(3, 7);
// 두 원소가 같은 집합에 속해 있는지 확인
System.out.pri1과 7이 같은 집합에 속하는가? true
1과 4이 같은 집합에 속하는가? true
1과 8이 같은 집합에 속하는가? false'Algorithm' 카테고리의 다른 글
| [Algorithm/Study] 7주차 - 백트래킹 (1) | 2024.11.16 |
|---|---|
| [Algorithm/Study] 6주차 - 그래프 (10) | 2024.11.10 |
| [Algorithm/Study] 4주차 - 트리 (0) | 2024.10.26 |
| [Algorithm/Study] 3주차 - 해시 (0) | 2024.10.19 |
| [Algorithm/Study] 2주차 - 스택과 큐 (0) | 2024.10.12 |



