| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 정보처리기사
- 스터디
- MySQL
- 자바
- 프로그래머스
- 혼공챌린지
- select
- 혼공단
- SQL
- doitandroid
- join
- Til
- 코틀린
- 자료구조
- java
- CS
- 오블완
- 기술면접
- 알고리즘
- 혼공파
- 정처기
- groupby
- 안드로이드스튜디오
- 인프런
- Kotlin
- Android
- 티스토리챌린지
- 카카오코테
- 코테
- 안드로이드
- Today
- Total
Welcome! Everything is fine.
[Java/Study] 김영한의 실전 자바 중급 2편 - 스터디 12회차 본문
인프런 강의 <김영한의 실전 자바 - 중급 2편>을 보고 정리한 내용입니다.
매주 모여 각자 정리한 내용을 기반으로 발표하고 질문 공유하는 스터디입니다.
📘빅오(O) 표기법
- 빅오(Big O) 표기법 : 알고리즘 성능을 분석할 때 사용하는 수학적 표현 방식으로, 데이터의 양의 증가에 따른 성능 변화 추세를 이해하기 위한 방법이다. 데이터가 매우 많이 들어오면 상수는 크게 의미가 없어지므로 빅오 표기법에서는 상수를 제거한다.
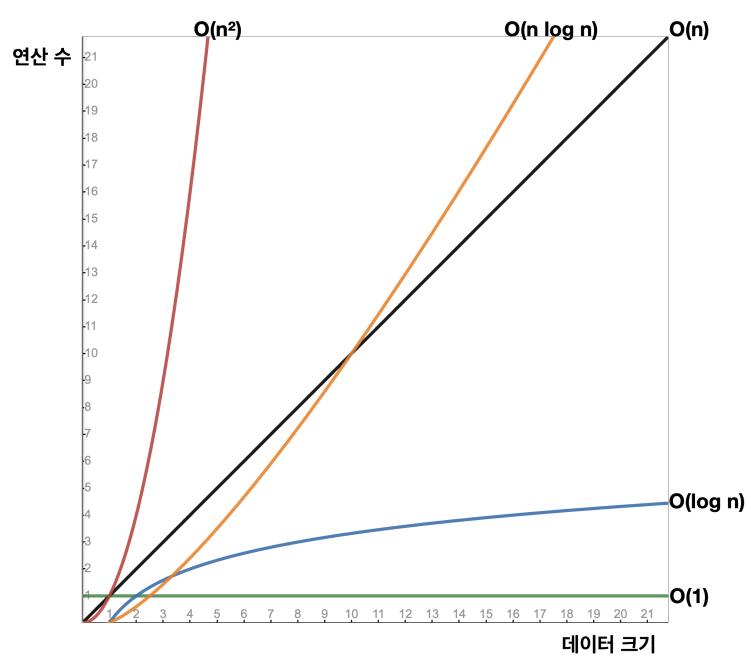
- O(1) : 상수 시간, 입력 데이터의 크기에 관계없이 알고리즘 실행 시간이 일정
- O(n) : 선형 시간, 알고리즘 실행 시간이 입력 데이터의 크기에 비례하여 증가
- O(n^2) : 제곱 시간, 알고리즘의 실행 시간이 입력 데이터의 크기의 제곱에 비례하여 증가
- O(log n) : 로그 시간, 알고리즘의 실행 시간이 입력 데이터의 크기의 로그에 비례하여 증가
- O(n log n) : 선형 로그 시간, 많은 효율적인 정렬 알고리즘
📘배열의 특징
배열은 인덱스를 통한 입력, 변경, 조회의 경우 한 번의 계산으로 자료의 위치를 빠르게 찾을 수 있다는 특징을 가진다. 하지만 배열에 들어있는 데이터를 검색하는 경우, 배열 안에 들어있는 데이터를 하나하나 비교하며 확인해야 한다. 따라서 배열의 크기가 클 수록 시간이 오래 걸린다.
즉, 다음과 같이 정리할 수 있다.
- 배열의 인덱스 사용 - O(1)
- 배열의 순차 검색 - O(n)
배열을 특정 위치에 추가한다면 어떨까? 결론부터 말하자면, 마지막 위치에 추가하는 것을 제외하면 그리 성능이 좋지 않다. 새로운 데이터를 입력할 공간을 확보하기 위해 기존의 데이터를 오른쪽으로 한 칸씩 밀어야 하기 때문이다.
- 배열의 첫 번째 위치에 추가 - O(n)
- 배열의 중간 위치에 추가 - O(n)
- 배열의 마지막 위치에 추가 - O(1)
// 마지막 위치에 추가
private static void addLast(int[] arr, int newValue) {
arr[arr.length - 1] = newValue;
}
// index 위치에 추가
private static void addaAtIndex(int[] arr, int index, int newValue) {
for (int i = arr.length - 1; i > index; i--) {
arr[i] = arr[i - 1];
}
arr[index] = newValue;
}
// 첫 번째 위치에 추가
private static void addFirst(int[] arr, int newValue) {
for (int i = arr.length - 1; i > 0; i--) {
arr[i] = arr[i - 1];
}
arr[0] = newValue;
}
이러한 배열은 다음과 같은 한계가 있다.
- 배열의 크기를 생성하는 시점에 미리 정해야 해서 배열의 길이를 동적으로 변경할 수 없다.
- 데이터를 추가하기 불편하다.
📘직접 구현하는 배열 리스트
배열의 단점을 보완해 동적으로 데이터를 추가할 수 있는 자료구조를 리스트(List)라 한다.
- 배열(Array) : 순서가 있고 중복을 허용하는 자료구조로, 크기가 정적으로 고정된다.
- 리스트(List) : 순서가 있고 중복을 허용하는 자료구조로, 크기가 동적으로 변할 수 있다.
강의에서는 점진적으로 여러 기능을 추가해가며 실습했지만, 블로그에는 그냥 바로 제네릭까지 적용한 코드만 가져왔다.
public class MyArrayListV4<E> {
private static final int DEFAULT_CAPACITY = 5;
private Object[] elementData;
private int size = 0;
public MyArrayListV4() {
elementData = new Object[DEFAULT_CAPACITY];
}
public MyArrayListV4(int initialCapacity) {
elementData = new Object[initialCapacity];
}
public int size() {
return size;
}
public void add(E e) {
if (size == elementData.length) {
grow();
}
elementData[size] = e;
size++;
}
public void add(int index, E e) {
if (size == elementData.length) {
grow();
}
shiftRightFrom(index);
elementData[index] = e;
size++;
}
private void shiftRightFrom(int index) {
for (int i = size; i > index; i--) {
elementData[i] = elementData[i - 1];
}
}
private void grow() {
int oldCapacity = elementData.length;
int newCapacity = oldCapacity * 2;
elementData = Arrays.copyOf(elementData, newCapacity);
}
@SuppressWarnings("unchecked")
public E get(int index) {
return (E) elementData[index];
}
public E set(int index, E element) {
E oldValue = get(index);
elementData[index] = element;
return oldValue;
}
public E remove(int index) {
E oldValue = get(index);
shiftLeftFrom(index);
size--;
elementData[size] = null;
return oldValue;
}
private void shiftLeftFrom(int index) {
for (int i = index; i < size - 1; i++) {
elementData[i] = elementData[i + 1];
}
}
public int indexOf(E o) {
for (int i = 0; i < size; i++) {
if (o.equals(elementData[i])) {
return i;
}
}
return -1;
}
public String toString() {
return Arrays.toString(Arrays.copyOf(elementData, size)) +
" size=" + size + ", capacity=" + elementData.length;
}
}
여기서 중요하게 생각하는 몇 가지를 뽑아본다면, 동적 배열을 만드는 부분과 index 위치에 데이터를 추가/삭제하는 부분인 것 같다.
✔️ 동적 배열 만들기
동적 배열을 만들기 위해 size가 배열의 크기와 같아지면 호출되는 grow() 메서드를 만들었다. grow() 메서드는 기존 배열을 복사해 새로운 배열을 만들고 배열의 크기도 2배로 늘려준다. 이때 Arrays.copyOf(기존배열, 새로운길이) 메서드를 사용해 새로운 길이로 배열을 생성한 후 기존 배열의 값을 새로운 배열에 복사한다.
private void grow() {
int oldCapacity = elementData.length;
int newCapacity = oldCapacity * 2;
elementData = Arrays.copyOf(elementData, newCapacity);
}
한 번 grow() 메서드가 호출될때 배열의 크기를 너무 적게 늘리면 grow() 연산이 자주 발생할 가능성이 높고, 또 한번에 너무 많이 늘리면 낭비되는 메모리가 많아질 수 있다. 따라서 보통은 50% 증가시키는 방법을 사용한다.
✔️ index 위치에 데이터 추가하기
특정 위치에 데이터를 추가하기 위해서는 특정 위치 기준으로 오른쪽으로 한 칸씩 밀어야 한다. shiftRightFrom() 메서드로 i번째에 i-1번째 데이터를 대입한다. 다 밀고나서 공간을 만들었으면 index 위치에 데이터를 넣고 size를 증가시킨다.
public void add(int index, E e) {
if (size == elementData.length) {
grow();
}
shiftRightFrom(index);
elementData[index] = e;
size++;
}
private void shiftRightFrom(int index) {
for (int i = size; i > index; i--) {
elementData[i] = elementData[i - 1];
}
}
✔️ index 위치의 데이터 삭제하기
특정 위치에 데이터를 삭제하는 것 역시 추가하는 것과 비슷하다. shiftLeftFrom() 메서드를 이용해 왼쪽으로 밀고, size번째(맨 마지막) 데이터는 null을 대입해 삭제한다.
public E remove(int index) {
E oldValue = get(index);
shiftLeftFrom(index);
size--;
elementData[size] = null;
return oldValue;
}
private void shiftLeftFrom(int index) {
for (int i = index; i < size - 1; i++) {
elementData[i] = elementData[i + 1];
}
}
배열 리스트의 장단점을 정리해보자면,
- 장점 : 인덱스를 이용한 조회가 빠르다, 데이터를 마지막에 추가하거나 삭제하는 것이 빠르다.
- 단점 : 데이터를 앞이나 중간에 추가하거나 삭제하는 것이 느리다, 데이터 검색 역시 느리다.
즉, 배열 리스트는 데이터를 순서대로 입력하고 순서대로 출력하는 경우에 가장 효율적이다.
📘노드와 연결
노드를 만들고, 각 노드를 서로 연결하는 방식으로 배열 리스트의 단점을 극복할 수 있다. 노드 클래스는 내부에 저장할 데이터인 item과, 다음으로 연결할 노드의 참조인 next를 가진다. 그리고 생성자와 toString()메서드를 가진다. toString()을 오버라이딩한 것은 노드를 출력할 때 [A -> B -> C] 와 같이 깔끔하게 나오게 하기 위함이다.
public class Node {
Object item;
Node next;
public Node(Object item) {
this.item = item;
}
// [A -> B -> C]
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
Node x = this;
sb.append("[");
while (x != null) {
sb.append(x.item);
if (x.next != null) {
sb.append(" -> ");
}
x = x.next;
}
sb.append("]");
return sb.toString();
}
}
노드를 연결해 다음과 같이 다양한 기능을 만들 수 있다. 이렇게 노드를 연결해서 사용하는 자료 구조로 만든 리스트를 연결 리스트라고 한다.
public class NodeMain1 {
public static void main(String[] args) {
// 노드 생성하고 연결하기: A -> B -> C
Node first = new Node("A");
first.next = new Node("B");
first.next.next = new Node("C");
System.out.println(first);
// 모든 노드 탐색하기
printAll(first);
// 마지막 노드 조회하기
Node lastNode = getLastNode(first);
System.out.println("lastNode = " + lastNode);
// 특정 인덱스의 노드 조회하기
int index = 2;
Node index2Node = getNode(first, index);
System.out.println("index2Node = " + index2Node.item);
// 데이터 추가하기
add(first, "D");
System.out.println(first);
add(first, "E");
System.out.println(first);
add(first, "F");
System.out.println(first);
}
private static void printAll(Node node) {
Node x = node;
while (x != null) { // 다음 노드가 없을 때 까지
System.out.println(x.item);
x = x.next;
}
}
private static Node getLastNode(Node node) {
Node x = node;
while (x.next != null) { // Node.next의 참조값이 null이면 노드의 끝
x = x.next;
}
return x;
}
private static Node getNode(Node node, int index) {
Node x = node;
for (int i = 0; i < index; i++) { // index의 수만큼 반복해서 이동
x = x.next;
}
return x;
}
private static void add(Node node, String param) {
Node lastNode = getLastNode(node);
lastNode.next = new Node(param); // 마지막 노드에 새 노드 연결
}
}[A->B->C]
모든 노트 탐색하기
A
B
C
lastNode = [C]
index2Node = C
데이터 추가하기
[A->B->C->D]
[A->B->C->D->E]
[A->B->C->D->E->F]📘직접 구현하는 연결 리스트
연결 리스트 역시 제네릭까지 적용한 코드만 가져왔다. 주석을 꼼꼼하게 달아놔서 이해하는데 문제는 없을 것이다.
public class MyLinkedListV3<E> {
private Node<E> first;
private int size = 0;
// 마지막에 데이터 추가 - O(n)
public void add(E e) {
Node<E> newNode = new Node<>(e);
if (first == null) {
first = newNode;
} else {
Node<E> lastNode = getLastNode();
lastNode.next = newNode;
}
size++;
}
// 마지막 노드 찾기
private Node<E> getLastNode() {
Node<E> x = first;
while (x.next != null) {
x = x.next;
}
return x;
}
// 특정 위치에 데이터 추가 - 앞: O(1) / 뒤&중간: O(n)
public void add(int index, E e) {
Node<E> newNode = new Node<>(e); // 노드도 함께 추가
if (index == 0) {
newNode.next = first;
first = newNode;
} else {
Node<E> prev = getNode(index - 1);
// 신규 노드와 직전 노드의 다음 노드 연결
newNode.next = prev.next;
// 직전 노드에 신규 노드 연결
prev.next = newNode;
}
}
// 특정 위치에 있는 데이터 찾아서 변경, 기존 값 반환 - O(n)
public E set(int index, E element) {
Node<E> x = getNode(index);
E oldValue = x.item;
x.item = element;
return oldValue;
}
// 특정 위치에 있는 데이터 삭제 - 앞: O(1) / 뒤&중간: O(n)
public E remove(int index) {
Node<E> removeNode = getNode(index);
E removedItem = removeNode.item;
if (index == 0) {
first = removeNode.next;
} else {
// 삭제 대상의 직전 노드 찾기
Node<E> prev = getNode(index - 1);
// 직전 노드의 다음 노드를 삭제 노드의 다음 노드와 연결
prev.next = removeNode.next;
}
removeNode.item = null; // 삭제 노드의 데이터 초기화
removeNode.next = null; // 노드도 함께 제거
size--;
return removedItem;
}
// 특정 위치에 있는 데이터 반환 - O(n)
public E get(int index) {
Node<E> node = getNode(index);
return node.item;
}
// 특정 위치에 있는 노드 찾기
private Node<E> getNode(int index) {
Node<E> x = first;
for (int i = 0; i < index; i++) {
x = x.next;
}
return x;
}
// 데이터를 검색하고, 검색된 위치를 반환 - O(n)
public int indexOf(E o) {
int index = 0;
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.item)) return index;
index++;
}
return -1; // 찾는 데이터가 없을 경우
}
// 연결 리스트 크기 반환
public int size() {
return size;
}
@Override
public String toString() {
return "MyLinkedListV1{" +
"first=" + first +
", size=" + size +
'}';
}
private static class Node<E> {
E item;
Node<E> next;
public Node(E item) {
this.item = item;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
Node<E> x = this;
sb.append("[");
while (x != null) {
sb.append(x.item);
if (x.next != null) {
sb.append(" -> ");
}
x = x.next;
}
sb.append("]");
return sb.toString();
}
}
}
연결 리스트에서 데이터를 추가할 때는 추가할 데이터의 위치를 노드를 타고 들어가 찾아야 한다. 따라서 만약 100개의 데이터 중 99번째에 데이터를 추가한다고 하면, 99번째 노드까지 타고 들어가야하는 것이다. 따라서 맨 앞에 추가하는 것이 아니라면 추가할 위치는 O(n)으로 느리게 찾게 된다.
데이터르르 추가하는 위치에 따라 어떻게 달라지는지 살펴보자. 삭제도 마찬가지이므로 추가만 가져왔다.
✔️ 첫 번째 위치에 데이터 추가 - O(1)
첫 번째 위치에 데이터를 추가하는 경우,
1) 신규 노드를 생성한다.
2) 신규 노드와 다음 노드(기존 첫 번째 노드)를 연결한다.
3) 첫 번째 노드를 가리키는 first에 신규 노드를 연결한다.
public void add(int index, Object e) {
Node newNode = new Node(e);
if (index == 0) { // 맨 앞에 추가되는 경우
newNode.next = first;
first = newNode;
} else {
Node prev = getNode(index - 1);
newNode.next = prev.next;
prev.next = newNode;
}
}
만약 배열이라면 데이터를 추가할 경우 모든 데이터를 오른쪽으로 밀어야 한다. 하지만 연결 리스트는 새로 생성한 노드의
참조만 변경하면 된다.
✔️ 중간 위치에 데이터 추가 - O(n)
중간 위치에 데이터를 추가하는 경우,
1) 신규 노드를 생성하고 노드가 입력될 위치의 직전 노드(prev)를 찾는다.
2) 신규 노드와 직전 노드(prev)의 다음 노드를 연결한다.
3) 직전 노드(prev)에 신규 노드를 연결한다.
public void add(int index, Object e) {
Node newNode = new Node(e);
if (index == 0) {
newNode.next = first;
first = newNode;
} else { // 중간에 추가되는 경우
Node prev = getNode(index - 1);
newNode.next = prev.next;
prev.next = newNode;
}
}
데이터를 추가할 때, 연결 리스트는 새로 생성한 노드의 참조만 변경하면 되지만 신규 노드가 중간에 들어갈 때는 위치를 찾는 것이 오래 걸린다. 노드를 추가하는 것은 O(1)이지만, 노드를 추가할 위치를 찾는데 O(n)이 걸리므로 둘을 합하면 O(n)이 걸린다.
✔️ 마지막 위치에 데이터 추가 - O(n)
마지막 위치에 데이터를 추가하는 것 역시 중간에 데이터를 추가하는 것과 비슷하다. 노드를 마지막까지 순회해야 마지막 노드를 찾을 수 있으므로 O(n)의 시간이 걸린다.
public void add(Object e) {
Node newNode = new Node(e);
if (first == null) {
first = newNode;
} else {
Node lastNode = getLastNode();
lastNode.next = newNode;
}
size++;
}
✔️ 배열 리스트 vs 연결 리스트
- 데이터를 조회할 일이 많고, 뒷 부분에 데이터를 추가해야 한다면 → 배열 리스트
- 앞 부분에 데이터를 추가하거나 삭제할 일이 많다면 → 연결 리스트
'Java' 카테고리의 다른 글
| [Java/Study] 김영한의 실전 자바 중급 2편 - 스터디 14회차 (0) | 2025.01.25 |
|---|---|
| [Java/Study] 김영한의 실전 자바 중급 2편 - 스터디 13회차 (0) | 2025.01.18 |
| [Java/Study] 김영한의 실전 자바 중급 2편 - 스터디 11회차 (0) | 2025.01.07 |
| [Java] 얕은 복사 vs 깊은 복사 - clone(), Arrays.copyof() (3) | 2025.01.02 |
| [Java/Study] 김영한의 실전 자바 중급 1편 - 스터디 10회차 (0) | 2024.12.29 |



